Análisis matemático de algunos juegos de magia
Antonio Javier Serrano Mora
Primavera de 2006
Resumen
Destripar trucos de magia nunca ha sido costumbre entre
magos, pero como yo sólo soy un matemático aficionado a la magia, supongo que
se me disculpará semejante atrevimiento. Este artículo trata de analizar la
causa de que algunos trucos de magia con cartas funcionen siempre,
independientemente de la calidad del mago. Aunque la buena presentación, la
atención de los espectadores, la expectación y la sorpresa final sólo los
buenos magos podrán conseguirla.
1 Vocabulario básico
Casi
Picas

Tréboles

Corazones

Diamantes

Oros

Copas

Espadas

Bastos

|
todos los magos usan para sus trucos de cartas la
llamada <<baraja francesa>>. Sus 52 cartas están repartidas en
cuatro <<palos>>, dos negros (picas y tréboles) y dos rojos
(diamantes y corazones), como se muestra al margen.
Cada palo está compuesto por 13 cartas: un
<<as>> (rotulada A), una <<jota>> (rotulada J), una
<<dama>> (rotulada Q), un <<rey>> (rotulada K) y nueve
cartas rotuladas con los números del 2 al 10, ambos inclusive, y cuyo nombre es
igual al número que lucen.
A veces se usa también la llamada <<baraja
española>> de 40 cartas. Consta de cuatro palos: oros, copas, espadas y
bastos y cada palo tiene 10 cartas: la <<sota>> (rotulada con el
10), el <<caballo>> (rotulada con el 11), el <<rey>>
(rotulado con el 12), el <<as>> (rotulado con el 1) y seis cartas
más rotuladas con los números del 2 al 7, ambos inclusive. Muchas veces, la
baraja española añade dos cartas, numeradas con el 8 y el 9, en cada palo,
convirtiéndose en una baraja de 48 cartas.
En la baraja francesa, se conocen como
<<figuras>> a la jota, la dama y el rey. En la española, las figuras
son la sota, el caballo y el rey.
En muchos de los trucos que veremos, es indiferente
usar una baraja u otra y, para los demás, son necesarias pequeñas adaptaciones
si cambiamos la baraja.
Llamamos <<cara>> de una carta a la parte
donde se representa la figura, con su número o letra y el palo. No hay dos
cartas con la misma cara. Llamamos <<dorso>> de una carta a la parte
contraria de la cara. Todas las cartas tienen el mismo dorso. Llamamos
<<mazo>> al montón que forman las cartas apiladas una sobre otra. La
posición natural del mazo es con todas las cartas orientadas de modo que sus
caras no sean visibles, apoyadas sobre una mesa o sobre una mano. La primera
carta del mazo es la que está colocada sobre todas las demás, de la que sólo
vemos su dorso. El dorso de la primera carta se llamará <<parte
superior>> del mazo. La última carta del mazo es la que tiene su cara
apoyada sobre la mesa o sobre la mano. La cara de la última carta se llamará
<<parte inferior>> del mazo. Si por alguna razón se necesitara
orientar el mazo en sentido contrario, con las caras de las cartas hacia arriba,
entonces lo denominaremos <<mazo invertido>>.
Cuando, de un mazo, se trasladan las n primeras cartas
desde la parte superior a la inferior, se dice que se ha dado un
<<corte>> a la baraja. Esta acción es muy usada en los trucos de
magia porque introduce un aparente desorden en el mazo. Más adelante se verá
que, efectivamente, el desorden es mínimo.
2 Adivinar una carta
Este truco es de
los más sencillos y, seguramente, de los más repetidos en las sobremesas
familiares, sobre todo por los niños.
2.1 Efecto
El mago mezcla bien las
cartas y las abre en abanico con el dorso hacia arriba para que un espectador
escoja una carta. Tras mirarla y memorizarla, el espectador la devuelve al
mazo.
El mago le da la posibilidad al espectador de cortar
la baraja cuantas veces desee. Una vez hecho, el mago va cogiendo las cartas,
una a una, y va formando con ellas un mazo invertido. Cuando aparece la carta
elegida por el espectador el mago se detiene anunciando su adivinación.
2.2 Truco mágico
Cuando el espectador
saca del abanico de cartas la elegida, y mientras la observa para memorizarla,
el mago tiene que hacer dos mazos con las cartas, uno en cada mano. Da igual que
estos mazos no sean exactamente iguales. Lo único importante es que el mago ha
de memorizar la última carta del mazo que tenga en su mano derecha. La
llamaremos carta <<chivata>>. Lógicamente, el mago ha de mirar con
todo el disimulo posible esta carta. Cuando el espectador ya ha memorizado la
carta elegida, el mago le ofrece el mazo de su mano izquierda para que la
coloque sobre él y después se coloca el mazo de la mano derecha sobre la carta
elegida. De esta forma, la carta chivata está colocada sobre la carta
elegida.
Después de que el espectador dé los cortes que estime
a la baraja, el mago va poniendo de cara las cartas. Sólo tiene que esperar a
que aparezca la carta chivata. Entonces, la siguiente carta en salir es la carta
elegida por el espectador. Si por casualidad la carta chivata saliera la última,
entonces la carta elegida es la primera que se sacó, es decir, la que en estos
momentos yace debajo del mazo invertido.
2.3 Truco matemático
La clave de este
truco reside en los cortes que se le dan a la baraja. Imaginemos un mazo de
cartas y éstas numeradas desde el 1 hasta el 40 de arriba hacia abajo (estamos
usando baraja española). Podemos recorrerlas todas en orden: de la primera
pasamos a la segunda, de ésta a la tercera... y cuando lleguemos a la última
pasamos a la primera otra vez, cerrando una especie de círculo. Considerar que
tras la última carta viene la primera es dotar al mazo de un <<orden
circular>>, cosa fundamental para comprender lo siguiente.
El mazo puede describirse mediante la sucesión de
números naturales M1={1,2,3,¼,39,40}
En un corte se escogen las n primeras cartas del mazo y se pasan a su parte
inferior. El mazo resultante puede describirse mediante la sucesión
M2={n+1,n+2,¼,39,40,1,2,¼,n-1,n}
Como se observa, el orden circular del mazo sigue siendo el mismo: tras la
carta 1 viene la 2, tras la 2 la 3..., tras la 40 la 1... Se puede afirmar,
entonces, que el orden circular de un mazo es <<invariante>>
mediante cortes de la baraja.
Lo anterior quiere decir que, por muchos cortes que le
demos al mazo, nunca conseguiremos separar la carta chivata de la carta elegida,
pues se trata de cartas consecutivas, como se explicó más arriba. La única forma
de separar ambas cartas es dejando la chivata al final del mazo, pero entonces
la elegida será la siguiente, es decir, la primera de todas.
3 El reloj
3.1 Efecto
El mago
Este truco se lo vi
hacer al dependiente
de la tienda
de magia
Mágicus de Barcelona.
Me gustó tanto que se
lo
compré inmediatamente.
|
pide a un espectador que piense un número, sin
decirlo, de los que aparecen en un reloj normal de agujas, es decir, un número
entero entre 1 y 12. Cuando el espectador lo ha pensado, el mago le entrega, en
un sobre, una predicción sobre una carta que elegirá el espectador más adelante
y le pide que se la guarde, sin leerla de momento, en el bolsillo.
Luego, el mago le entrega un mazo de cartas y le pide
que pase de la parte superior del mazo a la inferior tantas cartas como el
número que ha pensado sin que nadie lo vea. Una vez hecho esto, el espectador
devuelve el mazo y el mago coloca sobre la mesa las 12 cartas superiores, una a
una, para hacer un mazo con ellas, mientras que explica que va a formar un
reloj. El resto de cartas se dejan a parte, sobre la mesa, o se le pide a otro
espectador que, sin mirarlas, las guarde hasta que el mago se las vuelva a
pedir.
Para formar el reloj, el mago coloca la primera carta
del montón de 12 en el lugar imaginario que ocuparía el 1 de un reloj, la
segunda en el lugar del 2 y, así, hasta la carta 12 que se coloca en el lugar
habitual del número 12 en los relojes. Todas las cartas permanecen con el dorso
hacia arriba. El mago, entonces, le pide al espectador que diga en voz alta el
número pensado y que le dé la vuelta a la carta que ocupa ese lugar en el reloj.
La carta que aparezca es la carta elegida por el espectador.
En este momento, el mago solicita al espectador que
lea la predicción que tiene guardada en su bolsillo desde el principio del juego
y que diga en voz alta si acertó o no. El espectador, tras leer la predicción
del mago, se muestra dubitativo, desencantado incluso, pero termina por afirmar,
aunque a regañadientes, que el mago acertó la predicción. No le falta razón al
espectador, pues en la predicción el mago escribió: <<La carta que usted
eligió NO es la dama de corazones>>.
El mago, notando las dudas del espectador, entabla un
diálogo con él, de forma que éste termina por reconocer que la adivinación era
muy fácil, pues en toda la baraja sólo hay una dama de corazones y que, además,
el mago la podría haber quitado de la baraja para que no saliera. Entonces el
mago da el golpe final. Diciendo que no quitó la dama de corazones de la baraja
y que la probabilidad de que saliera no es tan baja como parece, comienza a
darle la vuelta a todas las cartas del reloj que aún están con la cara hacia
abajo. El espectador se va asombrando cada vez más: todas las cartas del reloj,
salvo la elegida, son la dama de corazones. Tras mostrar las once damas de
corazones que había en el reloj junto a la carta elegida, el mago voltea las
cartas del mazo que estaba apartado y, también, todas esas cartas son la dama de
corazones. La sorpresa del espectador llega a su máximo en este momento.
3.2 Truco mágico
Por supuesto se trata
de una baraja preparada. El mazo está compuesto por 51 damas de corazones y otra
carta distinta, digamos el 4 de picas. Al principio, el 4 de picas ha de estar
situado en el lugar número 13 del mazo. Lo demás consiste en seguir la
descripción del juego hecha más arriba. Es importante que nadie vea las caras de
las cartas porque se perdería la sorpresa final.
3.3 Truco matemático
Consideremos el
mazo formado por una baraja de 52 cartas. La carta número 13 del mazo es el 4 de
picas. El espectador elige las n primeras cartas del mazo y las pasa abajo.
Entonces, el 4 de picas avanza n posiciones en el mazo, es decir, se coloca en
el lugar número 13-n. Cuando el mago hace un montón de
12 cartas del mazo en la mesa, el efecto es que invierte su orden, de forma que
la primera carta pasa a ser la número 12, la segunda la número 11... y la carta
número m pasa a ser la 13-m. El 4 de picas, que estaba
en el lugar número 13-n pasa a ocupar el lugar número
13-(13-n)=n, es decir,
exactamente el número de cartas que pensó el espectador. Por eso el mago tiene
la seguridad de que la carta elegida es la única distinta de la dama de
corazones.
El hecho de colocar el 4 de picas en la posición 13 es
debido a que se necesitan 12 cartas para hacer un reloj y el truco queda bonito
presentado así. Pero el principio matemático usado sigue siendo válido para
cualquier número de cartas. Imaginemos que, en lugar de un reloj, el mago va a
hacer una figura para la que necesita N cartas. Entonces debe situar el 4 de
picas en el lugar N+1. De esta forma, cuando el espectador quite las n primeras
cartas del mazo (ahora n puede ser cualquier número entre 1 y N), el 4 de picas
pasará a ocupar la posición N+1-n y cuando el mago
invierta el orden de las N primeras cartas del mazo, el 4 de picas pasará a la
posición N+1-(N+1-n)=n.
Este principio puede ser usado al comienzo de
cualquier otro truco para <<forzar>> al espectador a que elija la
carta deseada por el mago.
4 Las tres anillas de papel
4.1 Efecto
El mago1 aparece ante el público con tres anillas
grandes de papel en la mano y unas tijeras. Anuncia que va a hacer un ejercicio
auténticamente peligroso y difícil. Coge una de las anillas y, con las tijeras,
la va cortando por su centro paralelamente a los lados de la anilla. Cuando
termina el corte, se producen dos anillas iguales que la primera pero de la
mitad de ancho.
El mago pide dos voluntarios que crean que pueden
repetir lo hecho por él, esto es: cortar la anilla de papel paralelamente a sus
lados. Cuando los voluntarios terminan de hacer el corte en las otras dos
anillas que trajo el mago al principio, la sorpresa es grande: uno de ellos
produce dos anillas enlazadas y el otro produce una sola anilla el doble de
larga.
4.2 Truco mágico
El mago debe preparar
previamente las anillas de papel. Tiene que recortar tres rectángulos de 4 cm de
ancho por 80 cm de largo, y, luego, con pegamento, debe pegar sus lados cortos
para confeccionar las anillas.
 Figure 1: Hay que recortar tres tiras de
papel
La diferencia entre unas anillas y otras está en la
forma de pegar los lados cortos de los rectángulos de papel. Para la primera
anilla, se pegan juntos los vértices señalados con la misma letra en la figura
1.
Para la segunda anilla, antes de hacer el pegado se le da media vuelta a uno de
los lados cortos del rectángulo, de forma que se peguen juntos los vértices
rotulados con distinta letra. Finalmente, para la tercera anilla, antes de hacer
el pegado se le da una vuelta completa a uno de los lados cortos del
rectángulo.
Figure 1: Hay que recortar tres tiras de
papel
La diferencia entre unas anillas y otras está en la
forma de pegar los lados cortos de los rectángulos de papel. Para la primera
anilla, se pegan juntos los vértices señalados con la misma letra en la figura
1.
Para la segunda anilla, antes de hacer el pegado se le da media vuelta a uno de
los lados cortos del rectángulo, de forma que se peguen juntos los vértices
rotulados con distinta letra. Finalmente, para la tercera anilla, antes de hacer
el pegado se le da una vuelta completa a uno de los lados cortos del
rectángulo.
Dada la longitud de las tiras de papel, las torsiones
realizadas en dos se las anillas resultan imperceptibles, sobre todo si se están
moviendo en todo momento.
El resto del truco se desarrolla tal y como se explicó
en la sección anterior. El mago no debe hacer nada más. Las tijeras y el papel
(y las matemáticas) harán el resto del trabajo.
4.3 Truco matemático
La anillas de
papel confeccionadas de la manera descrita tienen propiedades muy diferentes. La
primera es un anillo normal (un cilindro) con dos caras distintas. Que el papel
tenga dos caras distintas puede no sorprender a muchos, pero demostrar que las
tiene no es cosa sencilla.
Podemos comprobar que, efectivamente, la primera
anilla tiene dos caras de la siguiente forma. Ponemos la punta de un lápiz sobre
una cara y sin levantarlo y sin pasar por los bordes, intentamos llegar a la
otra. Es imposible. Hay dos dos caras.
La segunda anilla, que tiene media torsión, es la
famosa cinta de Moebius. Sólo tiene una cara. Puede comprobarlo el lector usando
el mismo método del lápiz descrito antes. En esta ocasión se comprobará que
puede recorrer todo el papel sin levantar el lápiz y sin pasar por los bordes.
Sólo haya una cara.
La tercera anilla es una cinta de Moebius con dos
medias torsiones (o una torsión completa). ¿Cuántas caras tiene? Quizá el lector
guste de entretenerse comprobándolo.
Otra de las diferencias entre las anillas es,
precisamente, el efecto de un corte longitudinal, cosa que se aprovecha en este
truco. Pruebe el lector a construir cintas de Moebius con más torsiones.
¿Cuántas caras tendrá una cinta con tres medias torsiones? ¿Y con cuatro? ¿Cuál
será el resultado de cortarlas longitudinalmente?
5 La suma rara
5.1 Efecto
El mago2 entrega a un espectador el mazo de cartas de la
baraja francesa para que las mezcle a conciencia. Le pide luego que escoja tres
cartas al azar y las ponga, separadas, sobre la mesa sin que el mago pueda
verlas. El mago explica que las cartas de la mesa valen tantos puntos como el
número que lucen (los ases valen 1) pero que las cartas que aún están en el mazo
valen un punto cada una.
A continuación, le solicita al espectador que, sobre
cada carta de las de la mesa haga un montón de manera que se completen 15 puntos
en cada uno de ellos. Por ejemplo, si el espectador eligió un 6, debe poner
sobre ella otras nueve cartas. Estas cartas ha de ponerlas boca arriba. El mago
tiene que permanecer de espaldas a la mesa para no ver nada.
Hecho todo lo anterior, el mago le pide al espectador
que cuente las cartas que aún le quedan en el mazo y que lo diga en voz alta.
Inmediatamente, el mago adivina la suma de las tres cartas que, al principio del
juego, fueron elegidas y que aún están boca abajo sobre la mesa.
5.2 Truco mágico
De la baraja francesa
deben quitarse las figuras y dejar, en cada palo, sólo el as y las cartas
numeradas entre 2 y 10. De esta forma el mazo tiene 40 cartas. También puede
usarse una baraja española de 40 cartas, anunciando que la sota valdrá 8 puntos,
el caballo 9 y el rey 10. Mejor todavía sería usar la baraja española sin reyes
ni caballos pero añadiendo los ochos y los nueves. Entonces, cada carta vale
tantos puntos como el número que luce.
Cuando el mago oiga el número sobrante de cartas que
aún están en el mazo del espectador, debe sumarle siempre 8. El resultado de
esta suma coincide con la suma de las tres cartas elegidas.
5.3 Truco matemático
Sean
n1, n2 y n3 los números de las cartas elegidas.
El mago trata de adivinar el valor de
S=n1+n2+n3. Una vez puestas en la mesa estas
tres cartas, en el mazo del espectador quedan M=37 cartas.
Sobre la carta que vale n1 puntos se
colocan 15-n1 cartas. Sobre la que vale
n2 puntos se colocan 15-n2 cartas
y, finalmente, sobre la que vale n3 puntos se colocan 15-n3 cartas, de forma que en el mazo quedan ahora:
| M=37-(15-n1)-(15-n2)-(15-n3)=(n1+n2+n3)-8=S-8 | |
Este número M es que el anuncia el espectador y se ve
de manera inmediata que el mago, sumándole 8, obtiene S.
Este truco puede admitir, en principio, variaciones
tanto en el número de cartas que el espectador debe colocar sobre la mesa como
en el número de puntos que cada montón debe alcanzar. Supongamos que sobre la
mesa se colocan k cartas de valores n1,n2,¼,nk. Supongamos además que cada montón debe
alcanzar los p puntos. Entonces, al final del truco, el espectador debe anunciar
el número:
| M=(40-k)- |
k
å
i=1
|
(p-ni)=40-k- |
k
å
i=1
|
p+ |
k
å
i=1
|
ni= | |
| =40-k-pk+S=40-k(1+p)+S=S-[k(1+p)-40] | |
El mago debe añadirle a este M la cantidad
T=k(1+p)-40 para obtener el valor de S. En el truco
anterior, donde k=3 y p=15, se obtiene T=8, pero si se decide hacer, por
ejemplo, k=2 montones para que cada uno alcance p=11 puntos, entonces el mago ha
de añadirle al número que anuncie el espectador la cantidad de T=-16.
El mago debe tomar la precaución de que siempre sea
posible realizar el truco, es decir, que no le falten cartas al espectador para
completar los montones. Para ello se tiene que cumplir que M ³ 0. Por tanto, S+40 ³ k(1+p) y de
aquí de obtiene que p £ [(S+40)/k]-1. Como p ha de cumplir esta inecuación para todos los
posibles valores de S, también lo tiene que hacer para su valor más pequeño,
esto es, k (en el supuesto que todas las cartas iniciales sean el as). De manera
que p £ [(k+40)/k]-1=[40/k].
Por otro lado, ha de cumplirse también que p ³ 10, pues de lo contrario podría ocurrir que uno de los
valores ni > p y no se podría completar este montón. Así que se
puede obtener la conclusión de que 10 £ p £ [40/k].
Obsérvese que el mayor valor que puede tomar k es 4.
Si k ³ 5 llegaríamos a la contradicción 10 £ p £ [40/k] £ 8. Para k=4 debe ser p=10. Para k=3 se obtiene 10 £ p £ 13, por tanto, el truco
propuesto tiene sus riesgos, no es completamente seguro, ya que en él se usan
los valores k=3 y p=15. Si imaginamos que las tres cartas iniciales son ases,
habría que poner sobre cada una de ellas 14 cartas, pero 3·14=42 > 40. ¡No
habría cartas para completar todos los montones! ¿Podría el lector calcular cuál
es la probabilidad de que le falle el truco al mago si lo propone con los
valores k=3 y p=15?
Para k=2 se obtiene que 10 £
p £ 20 y, finalmente, para k=1 se obtiene que 10 £ p £ 40.
La respuesta a la pregunta anterior no es muy
complicada. Las dos situaciones en las que el juego fallaría consisten en que
las tres cartas elegidas sean ases o bien que haya dos ases y un 2. Hay 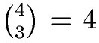 formas de elegir los tres ases y hay
formas de elegir los tres ases y hay 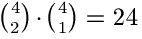 formas de elegir dos ases y un 2. En total,
hay 28 casos en los que fallaría el truco. Para sacar 3 cartas del mazo de 40
existen
formas de elegir dos ases y un 2. En total,
hay 28 casos en los que fallaría el truco. Para sacar 3 cartas del mazo de 40
existen ![]() formas distintas, de forma que la probabilidad pedida es
[28/9880] @ 0.003. Es decir, 3 de cada mil trucos
saldrán mal, riesgo que el mago podría asumir.
formas distintas, de forma que la probabilidad pedida es
[28/9880] @ 0.003. Es decir, 3 de cada mil trucos
saldrán mal, riesgo que el mago podría asumir.
Por otro lado, cuando el espectador anuncie que le
faltan cartas, el mago podría preguntarle entonces que cuántas le faltan. La
respuesta sólo puede ser 4 ó 5. En el primer caso el mago puede responder que
S=4 y en el segundo que S=3, saliendo airoso del trance y con un éxito total
porque, además, puede adivinar cuáles son las cartas que hay boca abajo
(salvo el palo).
6 Las 27 cartas
Este truco es muy
conocido y no existe sobremesa familiar que se precie en la que no se haya
presentado alguna vez. Aunque tiene diferentes nombres y se puede realizar con
distinto número de cartas, he preferido presentar dos versiones: la clásica y la
que se da en Tamariz (1991)3.
6.1 Efecto de la versión clásica
El
mago enseña a un espectador 21 cartas, previamente mezcladas, una a una,
disponiéndolas en tres montones. El espectador, sin que el mago lo vea, debe
anotar en un papel una de esas 21 cartas, la que desee. Luego, debe decirle al
mago el montón que contiene la carta elegida. El mago recoge los tres montones y
vuelve a repartir las cartas, cara arriba, en tres montones. El espectador debe
decir cuál de los montones contiene ahora su carta. De nuevo, el mago recoge los
montones y hace otra vez tres de ellos. El espectador dice nuevamente dónde está
su carta. El mago adivina la carta elegida.
6.2 Efecto de la versión de Tamariz
El
mago baraja bien un mazo de 27 cartas y las va mostrando una a una haciendo con
ellas tres montones. El espectador elige mentalmente (o anota en un papel) una
de las cartas y comunica al mago en qué montón se encuentra la carta elegida.
Entonces el mago mezcla bien uno de los montones, lo corta, lo da a cortar al
espectador y reúne los tres montones. Otra vez el mago muestra las cartas y hace
los tres montones. El espectador dice en cuál de ellos se encuentra su carta. El
mago mezcla bien dos de los montones, corta y da a cortar y unifica el mazo. Por
última vez, el mago repite el proceso de hacer los tres montones mostrando las
caras de las cartas. Cuando el espectador señala el montón que contiene la carta
elegida, el mago pide que se mezclen los tres montones por separado y luego
juntos y que se corten tantas veces como se desee. El mago, tocando las cartas
por el dorso, sin ver las caras, adivina la carta elegida.
6.3 Truco mágico de la versión
clásica
Cada vez que el espectador señale el montón que contiene la carta
elegida, el mago, al recomponer el mazo, debe tomar la precaución de colocarlo
entre los otros dos montones. Si se hace así las tres veces, la carta elegida
queda colocada en la posición 11 del mazo, es decir, justo en su centro.
El mago puede contar las 10 primeras cartas cara
arriba y anunciar que la siguiente carta será la elegida por el espectador.
6.4 Truco mágico de la versión de
Tamariz
Tamariz incluye en su versión más cartas, cortes y mezclas reales de
cartas, lo que le da un toque más mágico que la versión clásica, pero el
fundamento es el mismo, como se verá.
Tras hacer tres montones de nueve cartas y después de
que el espectador haya dicho el que contiene su carta, el mago coge cualquier
otro montón, lo mezcla o da a mezclar y lo deja caer sobre el señalado por el
espectador. El mago tiene que memorizar la carta que queda cara arriba en este
mazo. Supongamos que es el cuatro de copas. Coloca el tercer montón sobre estos
dos, corta la baraja y la da a cortar al espectador. El mago extiende las cartas
cara arriba y corta de forma que la única carta visible sea el cuatro de copas.
Como se puede observar, tras estas operaciones, el montón que contiene la carta
elegida queda en el centro del mazo, como en la versión clásica.
Ahora, con el mazo dorso arriba, el mago reparte otra
vez los tres montones enseñando todas las cartas. El espectador indica el montón
que contiene su carta. El mago coge uno de los otros dos montones y lo mezcla
bien, dejándolo luego sobre el que contiene la carta elegida. Otra vez el mago
memoriza la carta que queda visible en este mazo, por ejemplo el tres de
espadas. El mago coge ahora el tercer montón, lo mezcla y lo coloca sobre los
otros dos montones. Corta el mazo, lo da a cortar un par de veces y, de nuevo,
busca la carta chivata, el tres de espadas, para cortar de forma que sea la
única visible del mazo.
Otra vez con el mazo dorso arriba, se reparten los
tres montones. Al llegar a la sexta carta de cada montón, se echa descuadrada.
Lo mismo con la novena. Cuando el espectador anuncia el montón que contiene su
carta, el mago memoriza la quinta de ese montón: es la carta elegida. El mago
pide al espectador que mezcle cada montón y luego los tres juntos. Mientras que
comenta que es imposible adivinar la carta, puesto que se ha cortado y mezclado
varias veces, despliega las cartas de cara y, por su dorso, va pasando el dedo,
hasta que la magia lo hace detenerse en una de ellas, que es, por
supuesto, la elegida por el espectador.
En el libro mencionado4, Tamariz añade otra variante aún más
interesante bajo el epígrafe Nota para los matemáticos. Se trata de
hacer los tres montones, como antes, y pedirle al espectador que nos diga en qué
lugar (primero, segundo o tercero) quiere que coloquemos el montón que tiene la
carta elegida. Y esto las tres veces. Supongamos que dice el lugar M1
la primera vez, el M2 la segunda vez y el M3 la tercera,
con Mi variando entre 1 y 3. Entonces, se cumple que la carta se
encuentra en el lugar P=M1+3M2+9M3-12, contando siempre de arriba hacia abajo en el mazo
dispuesto con el dorso hacia arriba. A este resultado le pondremos el nombre de
Teorema de Tamariz.
6.5 Truco matemático
En ambas
versiones, la matemática funciona exactamente igual. Lo importante es que el
montón que contiene la carta elegida se coloca en el centro del mazo cada vez.
Los cortes y mezclas que propone Tamariz sólo alteran el orden de los otros dos
montones, pero no el de la carta del espectador.
Analicemos la versión clásica de 21 cartas. Las cartas
del mazo las numeraremos de 0 a 20. Una vez que se distribuyen en tres montones
por primera vez, podemos imaginar que las cartas forman una matriz de dimensión
7x3, donde las filas están numeradas de 0 a 6 y las columnas de 0 a 2. Cada
columna de esta matriz representa uno de los montones que se hacen con las
cartas. Supongamos que la carta elegida por el espectador ocupa la posición del
elemento af1,m1 de la matriz de cartas, es
decir, pertenece a la fila f1 de la columna m1. Cuando
rehacemos el mazo dejando la columna m1 en su centro, la carta
elegida ocupa la posición p1=7+f1. Dado que 0 £ f1 £ 6 se tiene que 7
£ p1 £ 13. Como
desconocemos el valor de f1 aún no podemos adivinar la carta
elegida.
Al distribuir de nuevo las cartas en tres montones, la
carta número k se coloca en la fila número E[[k/3]], donde E[x] es la parte
entera del número real x. Por tanto, la carta elegida está en la fila
f2=E[[(p1)/3]]. Dados los valores anteriores de
p1 se tiene que f2e{2,3,4}. Cuando
se rehace el mazo, dejando en su centro el que contiene a la elegida, ésta ocupa
la posición p2=7+f2 y, por tanto, p2e{9,10,11}.
Cuando, por tercera vez, se distribuyen los tres
montones, la carta elegida queda en la fila
f3=E[[(p2)/3]], de donde se obtiene que f3=3 en
todos los casos. Cuando el mazo es rehecho, dejando en su centro el montón de la
carta elegida, ésta ocupa la posición p3=7+f3=10, de forma
que es la undécima carta del mazo (recordemos que las cartas se numeran desde
0).
Para la versión de 27 cartas poco hay que cambiar
respecto a lo que ya se ha dicho. Las cartas ahora se consideran numeradas del 0
al 26. Entonces, si la carta se encuentra en la fila f1 (ahora
f1 varía entre 0 y 8), tras rehacer el mazo dejando en su centro el
montón que contiene a la carta elegida, ésta ocupa la posición
p1=9+f1, lo que significa que 9 £
p1 £ 17. Cuando se hacen los tres montones
por segunda vez, la carta elegida está colocada en la fila
f2=E[[(p1)/3]], cuyos posibles valores varían entre 3 y 5.
Al rehacer el mazo de la forma descrita, la carta elegida ocupa la posición
p2=9+f2 cuyos valores varían entre 12 y 14.
Finalmente, cuando se hacen los tres montones otra
vez, la carta elegida ocupa la fila f3=E[[(p2)/3]] cuyo
único valor es f3=4, por eso indica Tamariz que, una vez que el
espectador dice el montón que la contiene, la carta elegida ocupa la quinta
posición. En esta variante no se recompone el mazo de la forma anterior. Si se
hiciera, la carta elegida ocuparía la posición p3=9+f3=13.
Se trataría de la décimocuarta carta, es decir, la que ocupa la posición central
del mazo.
Veamos ahora una generalización del truco. Sea N el
número de cartas del mazo, siendo N=3n. Cada montón contiene n cartas numeradas
desde el 0 hasta el n-1. Tras hacer los tres montones,
supongamos que la carta elegida por el espectador está en la fila f1
con 0 £ f1 £ n-1. Cuando se rehace el montón por primera vez, la carta
elegida ocupa la posición p1=n+f1, cuyos valores varían
entre n y 2n-1.
Al hacer los tres montones por segunda vez, la carta
elegida se encuentra en la fila f2=E[[(p1)/3]], cuyos
valores varían entre E[[n/3]] y E[[(2n-1)/3]]. En el
mazo reunificado siguiendo las reglas del truco, la carta elegida ocupará la
posición p2=n+f2 donde n+E[[n/3]] £ p2 £ n+E[[(2n-1)/3]].
De lo anterior deducimos que
f3=E[[(p2)/3]] con
| E |
é
ê
ë |
3
|
ù
ú
û |
£ f3
£ E |
é
ê
ë |
3
|
ù
ú
û |
| |
y,
de aquí, tenemos que p3=n+f3. Si queremos que este valor
sea único para poder determinar así cuál es la carta elegida por el espectador,
tenemos que exigir también que f3 sea único, es decir, que
para
lo que debe cumplirse que
|
é
ë |
n+E |
é
ë |
2n-1
3
|
ù
û |
ù
û |
- |
é
ë |
n+E |
é
ë |
n
3
|
ù
û |
ù
û |
= E |
é
ë |
2n-1
3
|
ù
û |
-E |
é
ë |
n
3
|
ù
û |
£
2 | |
y, para esto, debe
cumplirse que (2n-1)-n £ 8 es decir n £ 9. Por tanto, cada
montón ha de tener, como máximo, 10 cartas y, por consiguiente, el mazo puede
ser como mucho de 30 cartas.
Demostraremos ahora el Teorema de Tamariz.
Éste afirma que si el montón que contiene la carta elegida se coloca en las
posiciones M1, M2 y M3 cada vez que se recogen
las cartas, con Mie{1,2,3}, entonces la carta
elegida se encuentra colocada en la posición
P=M1+3M2+9M3-12 del
mazo de cartas colocado dorso arriba. Supongamos que el mazo tiene 27 cartas,
numeradas, como antes, entre 0 y 26. Según la notación anterior, tenemos que
demostrar que p3=P-1.
Supongamos que la carta elegida se encuentra en la
fila f1, con 0 £ f1 £ 8 y que el espectador decide colocar el montón de la carta
elegida en el lugar M1 con 1 £ M1
£ 3. Al rehacer el mazo, la carta elegida ocupa la
posición p1=9(M1-1)+f1. Para lo que sigue, usaremos varias veces
la propiedad de la función E[x] que dice que si n es un entero y x un número
real, entonces E[n+x]=n+E[x].
Cuando el mago hace los tres montones por segunda vez,
la carta elegida se coloca en la fila
| f2=E |
é
ë |
p1
3
|
ù
û |
=E |
é
ë |
9(M1-1)+f1
3
|
ù
û |
= E |
é
ë |
3(M1-1)+ |
f1
3
|
ù
û |
= | |
de
donde obtenemos que la posición que ocupa al ser rehecho el mazo (colocando el
montón de la carta elegida en la posición M2) es
| p2=9(M2-1)+f2=9(M2-1)+3(M1-1)+E |
é
ë |
f1
3
|
ù
û |
| |
y,
por tanto, al hacer los tres montones por última vez, la carta elegida está en
la fila
| f3=E |
é
ë |
p2
3
|
ù
û |
=E |
é
ê
ë |
| 9(M2-1)+3(M1-1)+E |
é
ë |
f1
3
|
ù
û
|
3
|
ù
ú
û |
= | |
| =E |
é
ê
ë |
3(M2-1)+(M1-1)+ |
3
|
ù
ú
û |
=3M2+M1-4+E |
é
ê
ë |
3
|
ù
ú
û |
| |
y
como f1 varía entre 0 y 8, se tiene que E[[(f1)/3]] varía
entre 0 y 2, de donde obtenemos que E[[(E[[(f1)/3]])/3]]=0 y,
entonces f3=3M2+M1-4.
Finalmente, tras rehacer el mazo por tercera vez,
colocando el montón de la carta elegida en el lugar M3, se tiene que
la carta del espectador se encuentra en la posición
| p3=9(M3-1)+f3=9M3-9+3M2+M1-4=P-1 | |
como se
quería demostrar.
7 Las 25 cartas
Tras hacer varias veces
alguna de las variantes anteriores, me gusta hacerles a mis amigos el siguiente
truco, parecido en apariencia. Los amigos siempre quieren descubrir el secreto
del truco magia y disfrutan si lo hacen o si el truco falla, así que la mejor
manera de despistarlos es fingir que uno lo ha olvidado o que todo está saliendo
mal. El hecho de hacerlo tras los anteriores trucos desvía la atención de los
espectadores, quienes esperan algo parecido de verdad. Yo lo presento así.
7.1 Efecto
El mago distribuye un mazo
de 25 cartas en cinco montones de cinco cartas cada uno y el espectador elige en
secreto una de ellas. El espectador informa al mago sobre el montón donde se
encuentra ubicada la carta elegida. El mago da a barajar cada montón de cartas y
luego los recoge en el orden que el espectador le indique.
Otra vez, el mago distribuye las cartas en cinco
montones iguales y otra vez el espectador dice en qué montón se encuentra la
carta elegida. Cuando el mago está recogiendo los montones según las
indicaciones del espectador, las cartas se le caen sobre la mesa de forma
desordenada. El mago anuncia que así es imposible que el truco salga bien pero
que, de todas formas, para que no se sientan desencantados, elegirá una carta al
azar para ver si acierta. Entonces el mago señala exactamente la carta elegida
por el espectador.
7.2 Truco mágico
El mago, tras
distribuir las 25 cartas en los cinco montones iguales formando una matriz, debe
memorizar el lugar donde coloca el montón que contiene la carta elegida. Es
indiferente el orden en el que se recojan las cartas de este o de otro montón,
lo importante es mantener unido el montón principal (el que tiene la carta del
espectador). Incluso podría dar al espectador cada montón para que lo barajara,
introduciendo así más caos en ellos. Supongamos que se coloca el montón
principal en la posición n. Cuando, por segunda vez, el espectador le diga el
número de montón (supongamos que es el m), el mago debe buscar la carta que se
encuentra en el cruce de la fila n con la columna m. Ésa es la carta elegida por
el espectador. Lo que sigue en la descripción anterior es puro chanchullo para
despistar a los demás. También podría el mago fingir que mezcla accidentalmente
la baraja tras recoger los montones la segunda vez y, luego, buscar la carta en
cuestión de alguna forma mágica.
7.3 Truco matemático
Imaginemos las 25
cartas dispuestas en una matriz 5x5 y que el montón principal se coloca en el
lugar n, con 1 £ n £ 5, al ser
recogidas todas las cartas. El orden de las cartas es siempre el del mazo dorso
arriba. Una vez recogidas y redistribuidas en los cinco montones (columnas de
nuestra matriz), las cinco primeras cartas, que antes formaban un mismo montón,
van a parar todas a la primera fila; las cinco siguientes, que provienen del
mismo montón, forman la segunda fila y, así, cada antiguo montón forma una misma
fila. Esta acción de recoger las cartas y distribuirlas de nuevo tiene el
efecto, por tanto, de cambiar cada montón, cada columna, en una fila, es decir,
de trasponer la matriz. Si el montón principal ha sido colocado en el lugar n
del mazo, ahora ocupará la fila n de la nueva matriz. Una de las cinco cartas
que componen esta fila es la carta elegida.
Cuando el espectador, por segunda vez, informa al mago
del montón donde está ubicada su carta, le está diciendo la columna donde se
sitúa y, como ya sabemos su fila, sólo hay que buscar el cruce de ambas.
8 Las tres joyas
Este truco aparece en
Deveraux (1995), pero me he permitido modificarlo un poco para que se comprenda
mejor, sobre todo la última parte del truco mágico.
8.1 Efecto
El mago se presenta con
tres joyas u objetos: un anillo, una billetera y una cadena (o los pide al
público) y solicita la colaboración de tres voluntarios. A uno de ellos le
entrega un botón de una bandeja que tiene dispuesta para la ocasión, a otro le
entrega dos botones y al último le da tres botones.
Con el mago de espaldas, cada voluntario coge una de
las joyas. Luego, el mago le pide a la persona que cogió el anillo que retire de
la bandeja tantos botones como le fueron entregados, al que cogió la billetera
le pide que retire de la bandeja el doble de los que le fueron entregados y,
finalmente, al que cogió la cadena le pide que retire el cuádruple de los que le
dieron al principio. El mago, entonces, se vuelve y adivina cuál de los
voluntarios cogió el anillo, cuál la billetera y cuál la cadena.
8.2 Truco mágico
El mago debe preparar
una bandeja con 24 botones. Mentalmente, debe asignar a cada voluntario el
número de botones que le entrega. Entonces, tras realizar todo lo referido en el
efecto, el mago cuenta, de un vistazo, los botones que quedan en la bandeja.
Sólo hay seis posibilidades: 1,2,3,5,6 ó 7 botones. En
la tabla siguiente las presentamos todas con la solución del truco. Designamos
con las letras A, B y C los objetos anillo, billetera y cadena, respectivamente.
Con los números 1, 2 y 3 se designan los voluntarios, según recibieron al
principio del juego 1, 2 ó 3 botones.
| Quedan |
A |
B |
C |
| 1 |
1 |
2 |
3 |
| 2 |
2 |
1 |
3 |
| 3 |
1 |
3 |
2 |
| 5 |
3 |
1 |
2 |
| 6 |
2 |
3 |
1 |
| 7 |
3 |
2 |
1 |
Por ejemplo, si en la bandeja quedan 5 botones,
entonces el tercer voluntario tiene el anillo, el primer voluntario tiene la
billetera y el segundo voluntario tiene la cadena.
El principal problema con el que se enfrenta el mago
es el de memorizar la tabla anterior. En el libro mencionado, al anillo (allí es
reloj) se le asigna la letra A, a la billetera (allí es pulsera) se le asigna la
E y a la cadena (allí es alfiler de corbata) se le asigna la I. Para recordar la
tabla anterior se usa una lista ordenada de palabras, tales como
<<Café>>, <<César>>, <<Cádiz>>... cuyas
vocales nos dan la asignación de joyas. Por ejemplo, si en la bandeja quedan
tres botones, entonces el mago recupera la tercera palabra <<Cádiz>>
y deduce que el primer voluntario tiene el anillo, que el segundo tiene la
cadena y que el tercero, por eliminación, tiene la billetera.
El método que yo propongo es de tipo numérico. Sea R
el número de botones que quedan en la bandeja. Se trata de formar una terna con
los números 1, 2, 3 de la siguiente forma.
- Si R es par (2 ó 6) entonces colocamos el 2 en primer lugar (el
único par). Si R=2 (que es la menor de las dos
posibilidades), tras el 2 colocamos el 1 (la menor de las dos
opciones que nos quedan) y luego, claro, el 3. Pero si R=6 (la mayor
de las dos posibilidades), tras el 2 colocamos el 3 (la mayor de la
opciones que quedan) y luego, claro, el 1. De forma que obtenos la terna 213 o
bien la 231. Ordenados así los voluntarios sólo queda asignar al primero el
anillo, al segundo la billetera y al tercero la cadena.
- Si R es impar del grupo menor (1 ó 3), entonces la terna
empieza por 1 (el menor impar). Si R es el menor de estos dos, el
siguiente número de la terna es el 2 (el menor de los que quedan) y si R es el
mayor de estos dos, el siguiente número es el 3 (el mayor de los que quedan).
Así se forman las ternas 123 ó 132.
- Si R es impar del grupo mayor (5 ó 7) entonces la terna
empieza por 3 (el mayor impar). La segunda cifra de la terna se
calcula con el mismo criterio que antes. Se forman así las ternas 312 ó 321.
8.3 Truco matemático
Cuando a cada
persona le asignamos un número (1, 2 ó 3), a cada objeto una letra (A, B ó C) y
luego establecemos una correspondencia biunívoca entre números y letras, lo que
se produce es una ordenación de las letras, esto es, una permutación. Como hay
tres letras, existen 3!=6 formas distintas de ordenarlas.
Supongamos los números x1, x2 y
x3 donde xie{1,2,3} y donde
xi ¹ xj si i ¹ j. Supongamos, además, que la persona que se llevó el
anillo es la etiquetada con el número x1, que la que se llevó la
billetera es la etiquetada con x2 y que la que se llevó la cadena es
la etiquetada con x3.
Como el mago, al principio, entrega un botón a una
persona, dos a otra y tres a otra, en la bandeja que contenía 24 botones sólo
quedan 18. Además, se retiran de la bandeja
x1+2x2+4x3 botones. En definitiva, sobre la
bandeja, el mago ve R=18-x1-2x2-4x3
botones.
Los posibles valores de R, que dependen de las seis
permutaciones de tres elementos, se recogen en la siguiente tabla:
| A |
B |
C |
x1+2x2+4x3 |
R |
| 1 |
2 |
3 |
17 |
1 |
| 2 |
1 |
3 |
13 |
2 |
| 1 |
3 |
2 |
15 |
3 |
| 3 |
1 |
2 |
13 |
5 |
| 2 |
3 |
1 |
12 |
6 |
| 3 |
2 |
1 |
11 |
7 |
Como, en cada caso, el valor de R es diferente, se
puede establecer una relación biunívoca entre los valores de R y cada una de las
permutaciones, de manera que conociendo el valor de R puede determinarse la
permutación correspondiente. La forma de establecer esta relación puede ser
cualquiera de las dos descritas en el truco mágico u otra que al lector se le
ocurra.
Quizás alguna persona se extrañe de que el mago le
indique a la persona que cogió la cadena que retire cuatro veces el número de
botones que recibió en lugar de que retire tres veces esa cantidad, como podría
parecer más lógico. De esta manera tendríamos que R=18-x1-2x2-3x3. Puede entretenerse el lector en averiguar
por qué no puede hacerse así antes de leer el párrafo siguiente.
Para variar la cantidad de botones que cada voluntario
debe retirar de la bandeja, siempre en términos de múltiplos de los que
recibieron del mago, hay que tener en cuenta que los posibles valores de R han
de ser todos diferentes. Si dos de ellos fueran iguales, el mago no podría
distinguir entre dos permutaciones distintas y podría equivocar su
adivinación.
9 Forzar una carta
Muchos trucos de
cartas empiezan <<forzando>> una carta, es decir, haciendo que el
espectador elija una carta que el mago previamente tiene preparada. En la
sección llamada El reloj vimos una manera de forzar la carta que ocupa
la posición 13 del mazo. Veamos una forma de forzar la carta numero 10 del mazo
que aparece descrita en Tamariz (1991).
9.1 Efecto
El mago solicita a un
espectador que diga un número entre 10 y 20, excluidos estos. Cuando lo dice, el
mago hace un montón en la mesa con ese número de cartas, depositándolas una a
una. Entonces el mago entrega este montón al espectador y le pide que sume los
dos dígitos del número que dijo y que busque la carta que ocupa ese lugar en el
montón que le ha entregado. Ésa será la carta elegida por el especador y el mago
ya puede adivinarla en cualquier momento. Por ejemplo, podría hacer el
truco que aparece en Tamariz (1991). Tras forzar una carta, el mago da a mezclar
la baraja al espectador. Cuando la recupera las va volteando una a una para
ponerlas cara arriba sobre la mesa. En un momento dado aparecerá la carta
elegida, pero el mago sin inmutarse sigue colocando cuatro o cinco cartas más.
En ese momento anuncia que la próxima carta que va a voltear será la elegida por
el espectador. Puede incluso ofrecerle alguna apuesta para que sea más
interesante. El mago, por supuesto, no voltea la siguiente del mazo que tiene en
la mano; busca la carta adecuada entre las que ya están sobre la mesa.
9.2 Truco mágico
La carta elegida por
el espectador se encuentra ocupando la posición número 10 del mazo inicial, así
que el mago debe poner allí la carta que quiera que sea la elegida o bien
fijarse, disimuladamente, en la está en esa posición.
9.3 Truco matemático
Supongamos que el
espectador dice el número N=10+m con 0 < m < 10. Entonces, al hacer el
montón de N cartas sobre la mesa, se invierte su orden, de manera que la primera
carta pasa a ser la número N, la segunda pasa a ser la N-1 y, en general, la carta número k pasa a ser la carta
número N+1-k. En particular, la carta número 10 pasa a
ser la número N+1-10=N-9=10+m-9=1+m, es decir, justamente
la suma de las cifras del número N.
No habría problema en que el espectador eligiera el
número N=10, puesto que la carta elegida iría a la posición 10+1-10=1 coincidiendo éste con la suma de las cifras de N. En
cambio, si el espectador elige N=20 tenemos, por un lado, que la carta elegida
se quedaría en la posición número 20+1-10=11 y, por
otro lado, la suma de las cifras de N es 2. El truco fallaría.
10 El aceite flotante
Más que de un
truco de magia (en realidad no hay truco mágico aquí), se trata de un
experimento físico con explicación matemática. En Tamariz (1991), se presenta
dentro del apartado llamado Magia científica. El autor explica que
mucha gente piensa que los líquidos no tienen forma propia, sino que se adaptan
a la forma del recipiente, y que con este truco el mago conseguirá demostrarles
la verdadera forma de los líquidos.
Se llena un vaso pequeño
de aceite y de oliva y se coloca dentro de otro vaso más grande. Se vuelca sobre
el vaso grande, llevando cuidado de que no caiga sobre el pequeño, una cantidad
de alcohol suficiente para cubrir el vaso de aceite. Después, con una
cucharilla, se va añadiendo agua poco a poco. En un momento dado el aceite
saldrá del vaso pequeño y se quedará en equilibrio adoptando la forma de una
esfera.
10.2 Truco matemático
El alcohol es
menos denso que el aceite, de forma que cuando se añade alcohol el aceite
permanece tal y como está dentro del vaso pequeño. Pero el aceite es menos denso
que el agua, así que, conforme se va añadiendo agua, la fuerza de la gravedad
que actúa sobre el aceite va siendo compensada con el empuje que experimenta
hacia arriba (principio de Arquímedes) debido a la diferencia de densidades. En
algún momento, el empuje iguala a la gravedad (o la supera un poquito).
Podríamos entonces afirmar que, debido a la compensación entre estas dos
fuerzas, sobre el aceite no actúa ninguna. Entonces, el aceite, libre de fuerzas
tiende a optimizar su supercie exterior. Este es un hecho muy repetido en la
naturaleza, desde las células hasta los planetas. Resulta que la superficie más
pequeña que encierra un volumen dado es, precisamente, la esfera (por eso las
células, los planetas y el aceite de este vaso adoptan esta forma).
La bola de aceite se mantiene en equilibrio pero, si
queremos que ascienda, sólo hay que añadirle más agua. De esta forma el empuje
superará a la gravedad.
Footnotes:
1El
truco aparece en Deveraux (1995)
2El
truco aparece en Deveraux (1995)
3La
versión clásica de 21 cartas puede verse también en Deveraux (1995) con el
nombre de La Elegida
4Se
vende junto con un delicioso maletín de artículos de magia
Bibliografía
- Deveraux, Roger: Juegos de magia. M. E. Editores S.L. 1995
- Tamariz, Juan: El mundo mágico de Tamariz. Ediciones El Prado.
1991.
File translated from TEX by TTH, version 3.76.
On 16 Sep 2006, 23:31. Más algunas
modificaciones hechas por el autor del artículo. 
















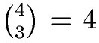 formas de elegir los tres ases y hay
formas de elegir los tres ases y hay 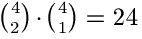 formas de elegir dos ases y un 2. En total,
hay 28 casos en los que fallaría el truco. Para sacar 3 cartas del mazo de 40
existen
formas de elegir dos ases y un 2. En total,
hay 28 casos en los que fallaría el truco. Para sacar 3 cartas del mazo de 40
existen